这么迟才学LCT。。人弱怎么办。。_(:з」∠)_。。。
LCT是可以解决动态树一类问题的数据结构，可以再均摊Nlog(N)的时间内进行Link,Cut,换根操作和维护链上信息。
先讲解一下LCT中的几个概念
称一个点被访问过，则刚对这个点进行了Access操作；
Preferred Child:对于一个节点u，如果最后访问的节点在其子树w中，则称w为u的Preferred Child，如果最后访问的节点为u本身，则u没有Preferred Child；
Preferred Edge:连接节点u与其Preferred Child的边；
Preferred Path:由Preferred Edge连成的路径；
我们可以显然的发现所有的Preferred Path会不重复地覆盖树上所有的点。。
根据这个性质我们可以对于每一条Preferred Path用一颗平衡树维护，称为Auxiliary Tree。用平衡树按照深度为关键字维护每一条Preferred Path，所有深度比当前点大的都在右子树中，所有深度比当前点小的都在左子树中。然后我们对于每一棵平衡树记录一下这颗平衡树中最高点的父亲，记为Path Parent，这样我们就可以用若干棵Auxiliary Tree表示原树了。
然后是LCT的几个操作：
Access(u) ：Access操作是LCT的基础，对一个点u进行Access操作后，它到根节点的边都变成Preferred Path；
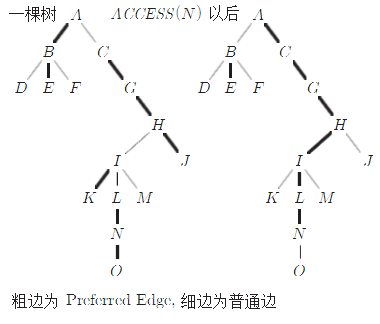
然后是实现问题：首先如果我们访问一个节点u则这个点的Preferred Child应该改为空。那么我们将它旋转到它所在的平衡树的根，将它的右子树与它分离。因为这个平衡树是以深度为关键字的，所以右子树中的点都是u的子孙节点。
接下来将根到它的路径都改为Preferred Path。如果当前点的平衡树并不包含根节点，设v为当前u所在平衡树的Path Parent，将v旋转到它所在的平衡树的根，然后将其右子树替换为u所在的平衡树，再更改一下原右子树的Path Parent。
关于复杂度，虽然看起来不正常。。但是均摊确实是Nlog(N)的。。。虽然我并不会证明。
Change_Root(u)：将这颗树的根换为x。这个那篇论文中并没有写到，然后不会。就被RXD大爷喷了。。_(:з」∠)_。。人生真艰难。其实自己YY一下就知道。先Access(u)，将u旋转到根，然后调换左右子树。这样就相当于改变了深度关系。
Link(x,y)：将两颗不相连的树通过在x，y之间连边的方式相连。先Change_Root(x)，然后将x所在的平衡树的Path Parent设为y就好了。
Cut(x,y)：将x，y之间的连边断开。将x换为根后，Access(y)，然后旋转到根，y的左儿子就是x，然后将两者的关系断开。
node *Access(node *x){
node *y;
for (y=null;x!=null;y=x,x=x->Fa) {Splay(x);x->R = y;x->Update();}
return y;
}
void Change_Root(node *x) {Access(x);Splay(x);x->Setrev();}
void Link(node *x,node *y) {Change_Root(x);x->Fa = y;}
void Cut(node *x,node *y) {Change_Root(x);Access(y);Splay(y);y->L = x->Fa = null;y->Update();}
2002: [Hnoi2010]Bounce 弹飞绵羊
Time Limit: 10 Sec Memory Limit: 259 MB
Submit: 6165 Solved: 3261
[Submit][Status][Discuss]
Description
某天，Lostmonkey发明了一种超级弹力装置，为了在他的绵羊朋友面前显摆，他邀请小绵羊一起玩个游戏。游戏一开始，Lostmonkey在地上沿着一条直线摆上n个装置，每个装置设定初始弹力系数ki，当绵羊达到第i个装置时，它会往后弹ki步，达到第i+ki个装置，若不存在第i+ki个装置，则绵羊被弹飞。绵羊想知道当它从第i个装置起步时，被弹几次后会被弹飞。为了使得游戏更有趣，Lostmonkey可以修改某个弹力装置的弹力系数，任何时候弹力系数均为正整数。
Input
第一行包含一个整数n，表示地上有n个装置，装置的编号从0到n-1,接下来一行有n个正整数，依次为那n个装置的初始弹力系数。第三行有一个正整数m，接下来m行每行至少有两个数i、j，若i=1，你要输出从j出发被弹几次后被弹飞，若i=2则还会再输入一个正整数k，表示第j个弹力装置的系数被修改成k。对于20%的数据n,m<=10000，对于100%的数据n<=200000,m<=100000
Output
对于每个i=1的情况，你都要输出一个需要的步数，占一行。
Sample Input
1 2 1 1
3
1 1
2 1 1
1 1
Sample Output
3
LCT模板，Link，Cut操作，Splay中只要维护子树大小即可
#include <cstdio>
#include <cstring>
#include <algorithm>
const int N = 200010;
using namespace std;
int n,num[N],Q,opt,x,k;
int read(){
int x = 0,f = 1,c = getchar();
while (c<'0' || c>'9') {if (c=='-') f = -1;c = getchar();}
while (c>='0' && c<='9') x = x*10+c-'0',c = getchar();
return x*f;
}
struct node *null;
struct node {
node *L,*R,*Fa;int S;
int Top(){return Fa==null || (Fa->L!=this && Fa->R!=this);}
void Update(){
if (this==null) return;
S = L->S+R->S+1;
}
void Zig(){
if (this==null) return;
node *y = Fa,*z = y->Fa;
if (z->L==y) z->L = this;else if (z->R==y) z->R = this;Fa = z;
y->L = R;if (R!=null) R->Fa = y;
R = y;y->Fa = this;y->Update();
}
void Zag(){
if (this==null) return;
node *y = Fa,*z = y->Fa;
if (z->L==y) z->L = this;else if (z->R==y) z->R = this;Fa = z;
y->R = L;if (L!=null) L->Fa = y;
L = y;y->Fa = this;y->Update();
}
} Nd[N];
void Splay(node *x){
while (!x->Top()){
node *y = x->Fa,*z = y->Fa;
if (!y->Top())
if (y->L==x) if (z->L==y) y->Zig(),x->Zig();else x->Zig(),x->Zag();
else if (z->R==y) y->Zag(),x->Zag();else x->Zag(),x->Zig();
else if (y->L==x) x->Zig();else x->Zag();
}
x->Update();
}
node *Access(node *x){
node *y;
for (y=null;x!=null;y=x,x=x->Fa){Splay(x);x->R = y;x->Update();}
return y;
}
void Link(node *x,node *y){
Access(x);Splay(x);x->L = x->L->Fa = null;
x->Fa = y;x->Update();
}
int main(){
null = Nd; n = read();
for (int i=0;i<=n+1;i++) Nd[i] = (node) {null,null,null,1};
null->S = 0;
for (int i=1;i<=n;i++) {
x = read();
if (i+x<=n) Nd[i].Fa = Nd+x+i;
}
Q = read();
for (int i=1;i<=Q;i++) {
opt = read();
if (opt==1) {
x = read()+1;
printf("%d\n",Access(Nd+x)->S);
}
else {
x = read()+1;k = read();
if (x+k>n) Link(Nd+x,null);
else Link(Nd+x,Nd+x+k);
}
}
}
3282: Tree
Time Limit: 30 Sec Memory Limit: 512 MBSubmit: 1033 Solved: 435
[Submit][Status][Discuss]
Description
给定Ｎ个点以及每个点的权值，要你处理接下来的Ｍ个操作。操作有４种。操作从０到３编号。点从１到Ｎ编号。
０：后接两个整数（ｘ，ｙ），代表询问从ｘ到ｙ的路径上的点的权值的ｘｏｒ和。保证ｘ到ｙ是联通的。
１：后接两个整数（ｘ，ｙ），代表连接ｘ到ｙ，若ｘ到Ｙ已经联通则无需连接。
２：后接两个整数（ｘ，ｙ），代表删除边（ｘ，ｙ），不保证边（ｘ，ｙ）存在。
３：后接两个整数（ｘ，ｙ），代表将点Ｘ上的权值变成Ｙ。
Input
第１行两个整数，分别为Ｎ和Ｍ，代表点数和操作数。
第２行到第Ｎ＋１行，每行一个整数，整数在［１，１０＾９］内，代表每个点的权值。
第Ｎ＋２行到第Ｎ＋Ｍ＋１行，每行三个整数，分别代表操作类型和操作所需的量。
Output
对于每一个０号操作，你须输出Ｘ到Ｙ的路径上点权的Ｘｏｒ和。
Sample Input
1
2
3
1 1 2
0 1 2
0 1 1
Sample Output
1
HINT
１＜＝Ｎ，Ｍ＜＝３０００００
#include <map>
#include <cstdio>
#include <cstring>
#include <algorithm>
const int N = 300010;
using namespace std;
int read(){
int x = 0,f = 1,c = getchar();
while (c<'0' || c>'9') {if (c=='-') f = -1;c = getchar();}
while (c>='0' && c<='9') x = x*10+c-'0',c = getchar();
return x*f;
}
int n,x,m,opt,y;
map <int,int> M[N];
struct node *null;
struct node {
node *L,*R,*Fa;int S,val,Xor,rev;
int Top() {return Fa==null || (Fa->L!=this && Fa->R!=this);}
void Down() {if (this==null) return;if (rev) {L->Setrev();R->Setrev();rev = 0;}}
void Setrev() {if (this==null) return;rev^=1;swap(L,R);}
void Update() {if (this==null) return;S = L->S+R->S+1;Xor = L->Xor^R->Xor^val;}
void Zig() {
if (this==null) return;
node *y = Fa,*z = y->Fa;
if (z->L==y) z->L = this;else if (z->R==y) z->R = this;Fa = z;
y->L = R;if (R!=null) R->Fa = y;
R = y;y->Fa = this;y->Update();
}
void Zag() {
if (this==null) return;
node *y = Fa,*z = y->Fa;
if (z->L==y) z->L = this;else if (z->R==y) z->R = this;Fa = z;
y->R = L;if (L!=null) L->Fa = y;
L = y;y->Fa = this;y->Update();
}
} Nd[N];
void Splay(node *x){
static node *S[N];node *tmp = x;int k = 0;
while (!tmp->Top()) {S[++k] = tmp;tmp = tmp->Fa;} S[++k] = tmp;
while (k) S[k--]->Down();
while (!x->Top()) {
node *y = x->Fa,*z = y->Fa;
if (!y->Top())
if (y->L==x) if (z->L==y) y->Zig(),x->Zig();else x->Zig(),x->Zag();
else if (z->R==y) y->Zag(),x->Zag();else x->Zag(),x->Zig();
else if (y->L==x) x->Zig();else x->Zag();
}
x->Update();
}
node *Access(node *x){
node *y;
for (y=null;x!=null;y=x,x=x->Fa) {Splay(x);x->R = y;x->Update();}
return y;
}
void Change_Root(node *x) {Access(x);Splay(x);x->Setrev();}
void Link(node *x,node *y) {Change_Root(x);x->Fa = y;}
void Cut(node *x,node *y) {Change_Root(x);Access(y);Splay(y);y->L = x->Fa = null;y->Update();}
void Extract(node *x,node *y) {Change_Root(x);Access(y);Splay(y);}
int Judge(node *x,node *y) {while (x->Fa!=null) x = x->Fa;while (y->Fa!=null) y = y->Fa;return x==y;}
int main(){
n = read();m = read();null = Nd;
for (int i=0;i<=n;i++) Nd[i] = (node) {null,null,null,1,0,0,0};
null->S = 0;
for (int i=1;i<=n;i++) Nd[i].val = read();
for (int i=1;i<=m;i++) {
opt = read();
if (opt==0){x = read();y = read();Extract(Nd+x,Nd+y);printf("%d\n",Nd[y].Xor);}
if (opt==1) {x = read();y = read();if (!Judge(Nd+x,Nd+y)) {Link(Nd+x,Nd+y);M[x][y] = M[y][x] = 1;}}
if (opt==2) {x = read();y = read();if (M[x][y]) {Cut(Nd+x,Nd+y);M[x][y] = M[y][x] = 0;}}
if (opt==3) {x = read();Nd[x].val = read();Splay(Nd+x);}
}
}
QTREE - Query on a tree
You are given a tree (an acyclic undirected connected graph) with N nodes, and edges numbered 1, 2, 3...N-1.
We will ask you to perfrom some instructions of the following form:
-
CHANGE i ti : change the cost of the i-th edge to ti
or - QUERY a b : ask for the maximum edge cost on the path from node a to node b
Input
The first line of input contains an integer t, the number of test cases (t <= 20). t test cases follow.
For each test case:
- In the first line there is an integer N (N <= 10000),
- In the next N-1 lines, the i-th line describes the i-th edge: a line with three integers a b c denotes an edge between a, b of cost c (c <= 1000000),
- The next lines contain instructions "CHANGE i ti" or "QUERY a b",
- The end of each test case is signified by the string "DONE".
There is one blank line between successive tests.
Output
For each "QUERY" operation, write one integer representing its result.
Example
Input:
1
3
1 2 1
2 3 2
QUERY 1 2
CHANGE 1 3
QUERY 1 2
DONE
Output:
1
3
修改边权，询问链Max。
放这道题的原因是这道题没有树形态的改变，对于链的询问论文中有写到一种比较简单（十分复杂）的方法，可以不用换根，所以Splay上就可以不用维护标记。
然而也是因为这个坑了我一天，学完以后发现并没有什么卵用，而且标记下传还十分蛋碎。
具体方法：先 Access(x)，然后在Access(y)的过程中，如果遇到的一颗Splay包含根节点，则当前这个点即为x和y的LCA，然后答案即为y所在Splay的答案和当前节点右儿子的答案。
这个方法唯一的好处就是，不用维护标记。
但是如果树的形态不变。。。为什么要用LCT呢。。。
所以总结。。这种方法好像并没有什么卵用。
但是代码还是这样写的。。。
#include <cstdio>
#include <cstring>
#include <algorithm>
const int N = 10010;
using namespace std;
int n,belong[N],x,y,s,I,val,head[N],cnt;
char opt[20];
struct data{int x,y,s,next,id;} e[N<<1];
int read(){
int x = 0,f = 1,c = getchar();
while (c<'0' || c>'9') {if (c=='-') f = -1;c = getchar();}
while (c>='0' && c<='9') x = x*10+c-'0',c = getchar();
return x*f;
}
struct node *null;
struct node {
node *L,*R,*Fa;int S,val,Max;
int Top(){return Fa==null || (Fa->L!=this && Fa->R!=this);}
void Update(){
if (this==null) return;
S = L->S+R->S+1;Max = max(max(L->Max,R->Max),val);
}
void Zig(){
if (this==null) return;
node *y = Fa,*z = y->Fa;
if (z->L==y) z->L = this;else if (z->R==y) z->R = this;Fa = z;
y->L = R;if (R!=null) R->Fa = y;
R = y;y->Fa = this;y->Update();
}
void Zag(){
if (this==null) return;
node *y = Fa,*z = y->Fa;
if (z->L==y) z->L = this;else if (z->R==y) z->R = this;Fa = z;
y->R = L;if (L!=null) L->Fa = y;
L = y;y->Fa = this;y->Update();
}
} Nd[N];
void Insert(int x,int y,int s,int id){
e[++cnt].x = x;e[cnt].y = y;e[cnt].s = s;
e[cnt].id = id;e[cnt].next = head[x];head[x] = cnt;
}
void dfs(int x,int fa){
for (int i=head[x];i;i=e[i].next)
if (e[i].y!=fa) {
Nd[e[i].y].val = Nd[e[i].y].Max = e[i].s;
Nd[e[i].y].Fa = Nd+x;
belong[e[i].id] = e[i].y;
dfs(e[i].y,x);
}
}
void Splay(node *x){
while (!x->Top()){
node *y = x->Fa,*z = y->Fa;
if (!y->Top())
if (y->L==x) if (z->L==y) y->Zig(),x->Zig();else x->Zig(),x->Zag();
else if (z->R==y) y->Zag(),x->Zag();else x->Zag(),x->Zig();
else if (y->L==x) x->Zig();else x->Zag();
}
x->Update();
}
node *Access(node *x){
node *y;
for (y=null;x!=null;y=x,x=x->Fa) {Splay(x);x->R = y;x->Update();}
return y;
}
void Work(node *x,node *y){
Access(y);
for (y=null;x!=null;y=x,x=x->Fa){
Splay(x);if (x->Fa==null) break;
x->R = y;x->Update();
}
printf("%d\n",max(x->R->Max,y->Max));
}
int main(){
null = Nd;
for (int T=read();T;T--){
n = read();
for (int i=0;i<=n;i++) Nd[i] = (node) {null,null,null,1,0,0};
null->S = 0;cnt = 0;
memset(head,0,sizeof(head));
for (int i=1;i<n;i++) {
x = read();y = read();s = read();
Insert(x,y,s,i);Insert(y,x,s,i);
}
dfs(1,-1);
while (~scanf("%s",opt+1)){
if (opt[1]=='D') break;
if (opt[1]=='Q') {
x = read();y = read();
Work(Nd+x,Nd+y);
}
if (opt[1]=='C') {
I = read();val = read();
node *t = Nd+belong[I];
t->val = val;t->Update();
Splay(t);
}
}
}
}
2016年1月10日 20:54
%%%%%%%%%%%%%%
2016年1月13日 13:15
噫，弹飞绵羊标算不是块状链表吗
2016年1月13日 16:02
@hzq84621: 难道不是一眼就知道是动态树吗。。
2016年1月16日 11:37
@hzq84621: Fuck you!
2016年1月16日 11:41
@Stalker: %小橙子干
2016年2月26日 19:49
我怎么觉得QTREE好像树剖就行了
2016年2月26日 19:57
@WasteRice: 我写这个主要是觉得不用换根可以提取区间很厉害。。。
2022年9月30日 01:56
Board of Secondary Education, Assam is known as SEBA is conducted the English subject examination tests along with all examination tests for all government and private schools General curriculum and vocational course students as Unit Tests, Term, three months (Quarterly), Assam HSLC English Question Paper six months (Half Yearly), Pre-Final and annual final public examination tests to the academic year of 2023.
2023年4月16日 18:19
How to Update/Register Your Cell Number with Indian Overseas Bank, The Reserve Bank of India’s guidelines are followed by the national bank Indian Overseas Bank. The bank has been providing its clients in the public banking sector with a wealth of convenient services and amenities. Indian Overseas Bank (IOB) Mobile Banking Registration, How to Update/Register Your Cell Number with Indian Overseas Bank, The Reserve Bank of India’s guidelines are followed by the national bank Indian Overseas Bank. ekhan.net The bank has been providing its clients in the public banking sector with a wealth of convenient services and amenities. Indian Overseas Bank (IOB) Mobile Banking Registration.