meepo's Blog

Input

Output

Sample Input

100 7
1 101 1 
2 1 2
2 2 3 
2 3 3 
1 1 3 
2 3 1 
1 5 5

Sample Output

3

Source

    这题我认为是今天做的比较有意义的一题吧（至少我知道了我学了半年还是连并查集都不会）。

    这题的基本思路是带权并查集，显然的是如果我们知道了A，B之间的关系和B,C之间的关系，我们就可以得到A,C之间的关系，我们就可以用并查集维护一个关系已知的集合。

    重点是怎样维护同一集合中的元素的关系，对于这个我们可以用带权并查集维护：

        对每个点x,维护他与他的父亲的关系dis[x]：

            dis[x] = 0：与父亲是同一种生物；

            dis[x] = 1：父亲可以吃他；

            dis[x] = 2：他可以吃父亲；

       设成这样的好处是我们可以根据输入中的d得到y到x的关系是d-1

       然后我们考虑路径压缩，可以容易得到的规律是对于一个点x和他的祖父的关系等于(dis[x]+dis[fa[x]])%3，可以用枚举来简单证明。

       现在我们可以维护集合内的信息了，然后我们考虑集合的合并。

       对于已知关系的两个点x，y，y到x的关系是d-1，a = fa[x],b = fa[y];

       可以求b到a的关系等于((3-dis[y])+(d-1)+(dis[x]))%3;

       如图：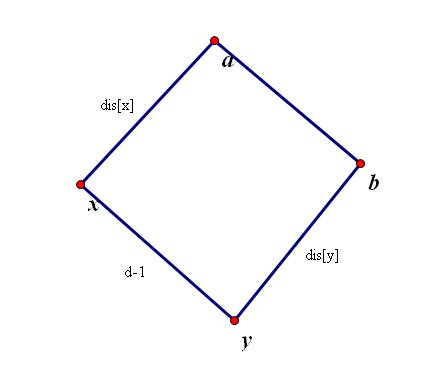

       我们可以从b到y，y到x，x到a的关系通过类似路径压缩的方法得到b到a的关系，其中（3-dis[y]）为b到y的关系，可以用枚举简单证明。

       最后就是求在同一集合中的数的关系是否符合输入，对于x和y，判断y到x关系是否是（d-1），就是判断dis[x]+(d-1)是否等于dis[y],可以通过如上的关系图理解。

       细节：我觉得这题并没有什么细节。。调试的时候唯一出错的是get函数没有return，这种神一样的错误我也是醉了

#include <cstdio>
#include <algorithm>
using namespace std;
int dis[500010],f[500010],sum,x,y,opt,n,k;
int get(int x){
	if (f[x]==x) return x;
	int Dis = dis[x],Fa = f[x];
	f[x] = get(f[x]);
	dis[x] = (Dis+dis[Fa])%3;
	return f[x];
}
int main(){
	scanf("%d%d",&n,&k);
	for (int i=1;i<=n;i++) f[i] = i,dis[i] = 0;
	for (int i=1;i<=k;i++){
		scanf("%d%d%d",&opt,&x,&y);
		if (x>n || y>n) sum++;
		else if (opt!=1 && x==y) sum++;
		else {
			int a = get(x),b = get(y);
			if (a!=b){f[b] = a;dis[b] = (3-dis[y]+(opt-1)+dis[x])%3;}
			else {
				if (opt==1)
					if (dis[x]==dis[y]) continue;
					else sum++;
				else if ((dis[x]+(opt-1))%3==dis[y]) continue;
				else sum++;
			}
		}
	}
	printf("%d",sum);
}